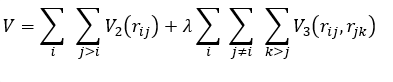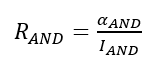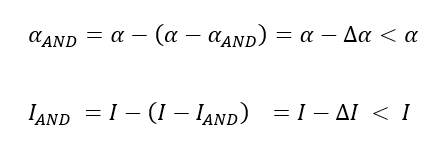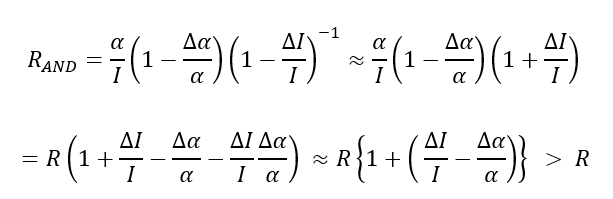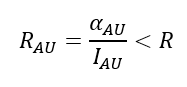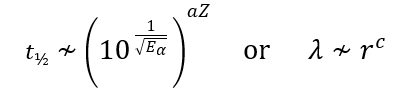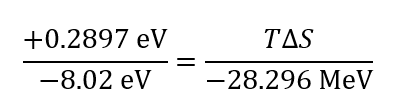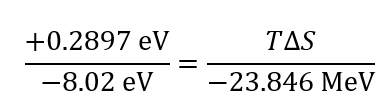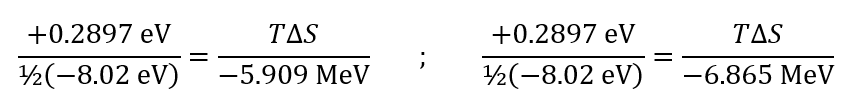Latent Heat Could Solve Accelerated Nuclear Decay’s Heat Problem—Part II

Latent Heat Could Solve Accelerated Nuclear Decay's Heat Problem-Part 2

Key Words: radiohalo, heat sink, latent heat, cooling, phase diagram, accelerated decay, uranium, polonium, nuclear decay, alpha cluster, condensed matter

Introduction: A Change of Phase for the Nucleus

As a novel solution to the heat problem associated with accelerating nuclear decay, herein described in the context of radiohalo production during an episode of accelerated decay, a spontaneous endothermic process, occurring inside each new ²⁰⁶Pb nucleus at the culmination of the ²³⁸U decay chain, is proposed. That is, an energy-absorbing phase change occurs in the newly formed lead nuclei at the radio-center thereby removing much of the heat just produced by the preceding chain of decays. The requisite latent heat for the phase change is taken [1] at Series' End from the adjacent rock where it is being deposited in rapid fire at a ring's radial distance away. This process is akin to an entropy increasing first-order phase transition between two condensed states of matter in (nonnuclear) chemistry like the melting of an ice cube ((∆G<0,∆H>0,∆S>0), here due to an abrupt change in the nuclear force (the mean field describing the nuclear potential) when the nuclide switches (crosses over) from being unstable to being stable with the last alpha decay in the uranium series (²¹⁰Po→²⁰⁶ Pb +α). It is assumed (or asserted) that only unstable nuclei are significantly affected by the change in the nuclear force (residual strong force that holds the nucleus together) responsible for accelerated decay. That is, the phase of stable nuclei remains a condensed fluid, consistent with the Liquid Drop Model and current scientific consensus, regardless of accelerated nuclear decay, while the unstable nuclei undergoing accelerated decay find themselves in an unknown lower entropy state.

So, like ice cubes cool a beverage by heat transfer from the beverage (as the cube's surroundings) to the ice, thereby melting the cubes, here the alpha clusters comprising an unstable nucleus undergoing accelerated decay would disassemble into nucleon pairs and sometimes dimers once they find themselves in a stable nucleus . As a phase transition, presumed to be first-order, this would absorb its latent heat from the surroundings, both the local rock matrix and any connate water in microfractures, thereby making the radio-center (i.e., its radiation-source nuclides) also a heat sink (i.e., its end-product nuclides) as a natural response to accelerated nuclear decay. So, the radio-center's unstable nuclei source the alpha particle bullets, the surrounding rock matrix heats up in stopping them, and the stable lead nuclei absorb the heat.

Parametrizing Phase Behavior

Phase behavior can be related to a factor λ found in the Stillinger-Weber class of potentials used in (classical) Molecular Dynamics and Monte Carlo simulations: 

which describes the relative weight of many-body [2] as compared with two-body interactions with V₂ modeling a steep repulsion plus short-range attraction (e.g., Lennard-Jones [3] or Morse [4] potentials) and V₃ a directional repulsion (e.g., Simple Harmonic [5] or Axilrod-Teller [6] potentials). This λ  is sometimes called tetrahedrality because "…the anomalies in [so called] tetrahedral liquids like water and Group XIV elements [would seem to] originate from the competition of the tetrahedral order [three-body contribution] which promotes the formation of low-density and low-entropy structures, and the pair (translational) order which promotes the formation of denser phases" [7] (Jabes et al., 2012). Alternatively, polar liquids like water might consist of relatively long-lived chains or large rings of its polar molecules embedded in a disordered network. [8] In any case, the phase at a particular pressure P and temperature T as derived from a Stillinger-Weber model potential depends on the value of the non-thermodynamic parameter λ, giving a three-dimensional λ-P-T diagram like the one shown in Figure 1 (Akahane et al., 2016). Here the low entropy phases are BCC, β-tin, dc, and sc16 solids (marked by their different crystal structures), and the high-entropy phase is a liquid (i.e., condensed fluid). Notice how much of phase space (P,T ) is subject to switching between liquid as high-entropy (everywhere above the multi-color blanket with purple trough) and a solid as lower-entropy (everywhere below it) with a change in λ, whether from liquid to BCC solid by its decrease or from liquid to dc/sc16 solid by its increase.

This phase-switching in relation to a parameter in the model potential is highly suggestive of how a nuclear potential with stronger many-body interactions (higher λ ) could mean a different phase describing the nuclei for large, unstable isotopes undergoing accelerated decay, though the precise forms of V₂ and V₃ would necessarily differ from those simulating so-called tetrahedral liquids in (non-nuclear) chemistry. An important difference, already acknowledged implicitly in discussing the alpha particle model of the nucleus, is the finite number of particles involved. [9] While the number of particles N in a molecular simulation (of say Ar or NaCl) must be large enough to rightly describe bulk behavior (with N→∞ effectively), the number of particles actually comprising the nucleus for even a large neutron-heavy isotope like is quite finite where the nuclear material's "charged molecules" are here asserted to be spin-antispin pairs with N~Z.¹⁰ [10] Thus, the phase diagram for each isotope's nucleus would be unique, depending not only on its λ but also on its particle number N (and therefore its mass): not only on the relative contribution of many-body vs. two-body forces for a particular many-body configuration but also directly on the size (N) of the system.

Insight from Helium's Nuclear Stability

Once normalized with respect to N, the nuclear material's λ for a given isotope might present experimentally as the ratio between the binding energy per nucleon of the alpha particle  and the binding energy per nucleon of the nuclide in question:

where R≡1 for the alpha particle itself. [11] It is herein suggested that if R exceeds a critical value then the nucleus would be in its lower-entropy phase comprised of pre-formed alpha particles as 4-clusters of nucleons (pairs of pairs) occupying adjacent (quantum) energy levels. Interpreting R in this way necessarily excludes nuclides that are too small - like those in front of the saturation plateau on the binding energy per nucleon curve - unless they are 4n (n alpha particle) nuclides like ¹²C and ¹⁶O with their characteristic peaks.

This critical value arguably lies near unity, between the ratios for long-lived uranium-238 on the low side and the very short-lived, surprisingly unstable beryllium-8 on the high side: 0.93445<R_crit<1.0016. The half-life of ⁸Be is so short ( (8.19×10^(-17)sec) [12] despite being a 4n nuclide that it can hardly be thought of as ever being anything but two pre-formed alpha particles [13] so beryllium-8's R is arguably above the critical value. [14] On the other hand, uranium inclusions (in zircons in biotite/mica in granitic rocks) made the halos for which the proposed phase change [15] must address the heat generation during accelerated decay so uranium-238's R lies below the critical value necessarily.

Note that the R-values for all the 4n nuclides (except for the highly unstable ⁸Be and the alpha particle ⁴He for which R is unity by definition), and all stable isotopes weightier than ¹²C, as well as all primordial isotopes and decay chain products that undergo alpha decay including ²³²Th and all the various poloniums, lie below that of ²³⁸U, as shown in the graph of ratio vs. mass number (Figure 2). [16] Again, understand that it is meaningless, in the spirit of an alpha particle model of the nucleus, to include low mass number nuclides (A≲40) in this graph unless they are 4n (A=2Z with Z even, or n alpha particles) obviously, the available nucleons cannot even make two alpha particles to interact with each other if the mass number is less than eight (A<8). Perhaps beryllium-8 is thus the only isotope with its nuclear material in the low-entropy state (strictly consisting of pre-formed alpha particles) under usual/natural conditions (not during an episode of accelerated decay) though it is questionable to speak of phase at all in the low-A  (pre-saturation) regime.

Enter Accelerated Nuclear Decay

Chaffin modeled accelerated decay (that is, a destabilization of long-lived nuclides) by shallowing the potential seen by the alpha particle and finding that a very small change in nuclear radius and/or barrier thickness at a critical well depth can shorten the half-life by many orders of magnitude - if/when it happens that the number of nodes (zeros) in the quasi-bound wave function decreases by one (Chaffin, 2005). This is a strictly quantum effect missed by the semi-classical formula which treats the alpha particle as a Gaussian wave packet, not a quasi-eigenstate, with its energy entirely kinetic. [17] In other words, a Gaussian wave packet does not have countable nodes in the same sense as an eigenstate. Rather, a numerical alpha/nucleon approach to modeling alpha decay finds the potential's parameters that give a quasi-bound eigenstate, [18] equating this energy [19] to that of the escaping quasi-bound alpha particle as determined from the mass difference. But the essential idea is that a small change in the strong force, manifesting itself in a changed potential well depth for the mean field seen by an alpha particle, would/must not appreciably affect the alpha particle's energy, thereby preserving the sizes (radii) and ordering of halo rings, per observation. And, it also would/must not otherwise affect regular chemistry (meaning the general behavior of materials) in any significant way since the Ark inhabitants survived, for one.

There is a very interesting anti-parallel in the literature wherein mainstream science (Adams and Grohs, 2016) considers what might be called decelerated nuclear decay (stabilization of a very short-lived nuclide) by proposing a small change in the strong force that would stabilize ⁸Be in an alternate universe (AU). It is implied that this would not affect regular chemistry there either, but only make nucleosynthesis in stars easier there compared to here. (Ironically, the hypothetical evolutionary mechanism of nucleosynthesis is thus unintentionally acknowledged as sketchy.) Interestingly, while ⁸Be is highly unstable in the sense that its half-life is exceedingly short ( 8.2×10^-17 sec), it can also be seen as barely not stable in the sense that its quasi-bound (non-negative) alpha particle's ground state energy is small (+81.8 keV). Here, a small change in one sense (slight deepening of the nuclear potential) arguably effects an infinite change in another sense (a nearly zero half-life becomes infinite). If it is scientific for the godless to ponder decelerated nuclear decay in their quest for aliens in an AU, it is no less scientific for the godly to ponder an episode of accelerated decay in the actual created universe where the Triune God who holds the nucleus together in the first place (Col. 1:17) can surely tweak His gluons for a short time. The author hereby keeps fashion with Saint Augustine in "plundering the Egyptians" (Ex. 3:22) for "Whatever has been rightly said by the heathen, we must appropriate to our uses" ( On Christian Doctrine, Book II, Ch. 40). Thus, an episode of accelerated decay can be seen as a temporal AU of sorts, due to God's intervention rather than a fictitious contrivance of an atheistic cosmogony.

The change in the strong force causing accelerated decay and manifesting as a shallowing of the nucleon potential wells (the mean fields seen by a neutron or a proton) to varying degrees depending on the isotope, would also manifest as a shallowing of the alpha particle potential well (the mean field seen by an alpha particle), but the effects would not necessarily be the same in degree. So, how might the ratio R be expected to change during an episode of accelerated decay? Given that the nuclear force is itself a residue of the strong force, with alpha particles here viewed as assemblages of charged molecules (pairs of pairs) and thus secondarily residual, it seems reasonable that the numerator of this ratio:

(where BE stands for binding energy) would decrease less in relative terms than its denominator; that is, that the attraction between nucleon pairs, strong as it is, would weaken less than the attraction or "bond" between nucleons, also in relative terms. In other words, the more residual the force, the smaller the net effect at the top from a change at the bottom, so to speak. Let the ratio of the alpha particle's binding energy per nucleon to a particular isotope's binding energy per nucleon during the Flood-Year episode of Accelerated Nuclear Decay (AND) be:

Then write numerator and denominator in terms of the normal (non- AND) values, as follows:

where∆α=|∆α|≥0 and ∆I=|∆I|≥0, being defined for a change in the strong force that shallows the potential wells. For small relative changes with   , it follows that:

This increase in R for long-lived isotopes experiencing accelerated decay and thus (further) destabilizing, is consistent with beryllium-8's high ratio ( R>1) when seen as two marginally connected alpha particles.

In effect, during the accelerated decay episode, the distinctive peak for helium in the binding energy per nucleon vs. mass number curve would likely reach all the way up to the saturation plateau ( (~8.8 MeV ) rather than falling short ( 7.1 MeV ) as it does under normal conditions (not during an episode of accelerated decay). On the other hand, the opposite scenario with a shortened helium peak in the binding energy curve and:

might describe that hypothetical AU where beryllium-8 is stabilized (i.e., for a change in the strong force that deepens the potential wells) and for∆α=-|∆α| and ∆I=-|∆I|.

Assume that uranium-238's new ratio during an episode of accelerated decay exceeds the phase-critical value ( R_AND>R_crit ), thus indicating a lower-entropy phase for its nuclear material characterized by pre-formed alpha particles with P≈100% vs. something like 2%≲P≲20% (Duarte and Siegel, 2010). Conceivably, this would eliminate the hindrance to preformation characterizing the higher-entropy (less-structured?) phase, thereby accelerating decay over Chaffin's node-change acceleration by some factor. Chaffin's modeling shows up to eight orders of magnitude decrease in half-life (Chaffin, 2005, p. 532) so adding this effect could net the nine needed for U-halos and Po-halos to form simultaneously in a matter of days. Coming at this from the other side suggests the same effect: when variant modeling gets other things right (e.g., energy levels and electromagnetic moments) but drastically overpredicts half-lives, as for extremely short-lived isotopes like polonium-212 ( t_½=299 ns ), an "extended shell model" that incorporates an hypothesized surface alpha clustering "find[s] a great amount of enhancement (three orders of magnitude) in the calculated alpha decay width" [20] (Tonozuka and Arima, 1979, p. 46).

Now suppose that the new ratios for all successive unstable daughters in the decay series (whether uranium or thorium) also exceed the phase-critical value until the final stable daughter product is reached at which point R has dropped below this value , since stable nuclides are presumed to be unaffected by accelerated decay in all essentials. The hypothesized increase in R during an episode of accelerated decay would push the ratio vs. mass number curve upward, and a just-so increase would put its tail (after the stable isotopes of lead) above the phase-critical value at/near unity (Figure 2). The large unstable nuclei including ²³⁸U, ²³²Th, ²¹⁰Po, etc., would thus be in the hypothetical lower-entropy phase while undergoing accelerated decay . The ensuing Chain's End phase change would thus cool each halo from the inside out , one lead nucleus at a time, concurrent with the halo's formation, by taking from the immediate environment the latent heat for each newly formed lead nucleus to resume its normal (higher-entropy) state.

Importantly, this idea must assume there would be no heat exchange (no thermodynamical considerations) directly associated with the miraculous turning on/off of accelerated decay, only the heat produced indirectly, when the decay products are slowed to a stop in the rocks, followed by the cooling at Decay Chain's End occurring naturally during the (miraculous) episode of accelerated decay, as described. In other words, the affected unstable nuclei just find themselves in the lower-entropy state consistent with the supernaturally changed strong force, not unlike like Lazarus found himself undead miraculously, without any consideration of the thermodynamics of his abrupt switch to the much lower-entropy state of being alive vs. dead. Likewise, the cooling effected by the lead's nuclear phase change being a natural outcome under special circumstances is like when the resurrected Lazarus died a second time, and (again) his body would have stunk in the tomb (Jn. 11:39) in keeping with thermodynamics (Second Law) and the local climate.

To quantify the thermal energy involved requires knowing how many alpha particles (alpha clusters) are potentially present within the stable lead-206 "core" of the decaying uranium series nucleus, being in the low-entropy state with quasi-bound alpha particles spilling (or furiously tunnelling) out. Having 42 excess neutrons, about 20 of which form the neutron skin, there remain 41 pairs of neutrons and 41 pairs of protons ( 42+4×41=206 ) to form 41 alpha clusters. From the nuclear surface inward (geometrically and energetically), think quasi-bound protons and resonant neutrons with small positive energies, then bound nucleons with increasingly negative energies, filling separate neutron and proton wells per the nuclear shell model for a nucleus in its ground state, as shown (Figure 3) for with its stable core.

Necessarily, the order of decays [21] is preserved during the episode of accelerated decay which also means tunneling occurs one alpha particle at a time; however, rapidly successive decays might occur. [22] Thinking in terms of a liquid droplet for the nucleus, only the alpha particle residing on/at the surface [23] can escape by evaporation, corresponding to the outermost quasi-bound level(s)/orbital. In effect, pre-formed alpha particles that are lower in the quasi-bound line-up, having smaller positive energies (so less unstable in the energy sense), cannot get out and away for lack of access to the surface. Thus, each decay can only be said to have a half-life (quantifying instability in the time sense) once its immediate parent is in being at which point the new outermost level corresponds to the new outgoing alpha particle. As previously stated, the general trend through a decay series has E_α increasing (and half-life decreasing), though there can be hiccups, as apparent from the outermost ring (most energetic alpha particle) of a U-halo corresponding not to ²¹⁰Po as last in the chain but to ²¹⁴Po. Barring such hiccups, the increase in the top-level energy with successive alpha decays, reflected in increasing halo ring radii, derives from the step-down in well depth [24] with each decay as the nucleus gets smaller (mass number decreases) [25] while the half-lives (decay rates) during accelerated decay collapse to within a few orders, if not the same order, of magnitude in flagrant noncompliance with Geiger-Nuttall; that is,

where t_½ and λ are half-life and decay rate respectively, r is the alpha particle’s range in air (or radius in a radiohalo), and a, c are positive constants for a given medium and parental Z.

It is an interesting exercise (Figure 4) to place the 146 neutrons and 92 protons for ²³⁸U, by spin-antispin pairs (↿⇂), in their respective nuclear shell model energy levels/states, per the usual filling rules [26] (Meyerhof, 1967, p. 56), with the well of neutrons starting deeper enough to top out the same as the proton well for the stable core isotope ²⁰⁶Pb (with its 124 neutrons and 82 protons), leaving 22 neutrons and 10 protons to occupy resonances or quasi-bound states (for neutrons or protons, respectively) where these 32 nucleons with positive energies (the green boxes) are the 8 alpha particles and 10 beta particles loosed in the uranium-238 decay chain. This suggests which nucleon pairs, having similar energies (a common hybrid orbital?), might organize into as many as 41 bound alpha particles (or alpha clusters), above the 21 neutron pairs (the blue boxes) at the bottom .

Cooling that is commensurate with the 43.7 MeV of heat from friction produced by stopping the eight alpha-particle “bullets” in the uranium series (or 37.5 MeV for stopping six alphas in the thorium series)[27] would thus be about an MeV of latent heat per alpha cluster in lead’s nucleus. While about 20% more cooling is needed if the beta decays are included, [28] less is needed if the adiabatic heating assumption is relaxed somewhat (i.e., some of the heat dissipates) suggesting that about an MeV per alpha particle of latent heat is still enough cooling to avoid halo-loss and/or allow halo formation; that is, to keep from exceeding the halo-bearing rock's annealing temperature, recalling that, without cooling, the temperature rise for one uranium halo is enormous (thousands of degrees Celsius). While uranium halos, in parenting polonium halos (per the transport model), do thereby lose some of their coolant, so to speak, they also generate commensurately less heat, with a subset of their most energetic alpha particles (the polonium emissions) being displaced to new radio-centers; [29] that is, the uranium radio-center does not fully contain its progeny due to parenting polonium halos. Thus the coolant, or heat sink, is located precisely where it is needed, whether at the radio-center for a U-halo or a Po-halo.

For comparison to a tentatively analogous phase change, [30] consider sodium chloride's latent heat of de-fusion per formula unit NaCl vs. its lattice energy (the energy released when gaseous ions unite into the lattice) in relation to what might be a corresponding quantity for nuclear material:

where the lattice energy for the nuclear material is taken to be the alpha particle's binding energy. This gives ∆H=T∆S=1.0 MeV; that is, about an MeV per alpha particle. Or, since anion and cation correspond to nucleon pairs for this analogy, the lattice energy for the nuclear material might be the alpha particle's binding energy minus the energy bound up in two deuterons: [31] -28.296 MeV-2(-2.225 Mev)=-23.846 MeV. . Then the relation becomes:

giving ∆H=T∆S=0.86 MeV ; that is, about an MeV per alpha particle. Alternatively, consider sodium chloride's latent heat of melting (de-fusing) per formula unit vs. its latent heat of de-vaporization (half its lattice energy) [32] in relation to two options for the corresponding quantity for the nuclear material:

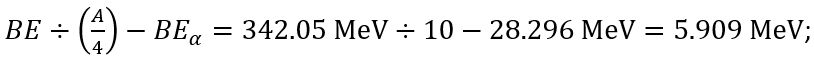
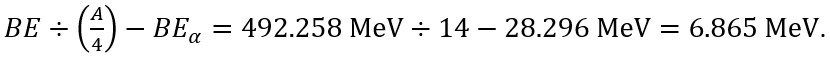
This being the difference between a saturation value for the binding energy (BE) per quad of nucleons [33] and the alpha particle's BE of 28.296 MeV. For ⁴⁰Ca as the largest stable 4n nuclide: ; while for ⁵⁶Fe at the top of the binding energy curve: . While these comparisons give ∆H of 0.43 to 0.50 MeV,  a hypothetical salt for which the latent heat of vaporization is a smaller fraction of its lattice energy is arguably more analogous to the nuclear material; and having say ¼ instead of ½ in the above denominators gives a ∆H_fus of 0.85 to 1.0 MeV; that is, about an MeV per alpha particle.

Certainly, it is not claimed that nuclear material being like a molten salt as to its relative latent heat is a rigorous analogy. Rather, it is a way to get at an order of magnitude value for the latent heat that might be associated with disassembling alpha clusters into nucleon pairs in lead's nucleus-whether for the uranium series or for the thorium series-per the proposed first-order phase change occurring at/with that final decay in the series during an episode of accelerated decay. Importantly, the disassembly of lead's arguably 41 alpha clusters, by this analogy, would seem to provide enough cooling to address the heat problem for radiohalos. In other words, the idea merits further investigation (via computer modeling?).

It is admittedly hard to think of a nucleus like ²⁰⁶Pb, consisting of only around a hundred nucleon pairs (21+41 pairs of neutrons and 41 pairs of protons but only 41 paired pairs), as undergoing a phase transition when a material's phase is generally understood to be a bulk property (infinite particle limit: N→∞). In molecular dynamics simulations in which bulk properties emerge for for large N and the N-dependence vanishes, for a small (low-N) system, the phase diagram (i.e., the graphical loci of coexistence lines) depends strongly on N . For a sodium chloride nanocrystal in the "cluster regime" [34] ( N<500 ), the internal energy distribution becomes bimodal near the melting temperature, meaning the system oscillates between its higher- and lower-entropy phases (Breaux et al., 2004) not unlike the phases in a two-component system. Consider again the alpha decay preformation factor which as a probability "…represents the fraction of the time two neutrons and two protons behave as a single alpha particle" (Duarte and Siegel, 2010). Perhaps alpha particles are transitory in nuclei because the natural state of the nucleus corresponds to such an oscillating two-phase region. The proposed phase change for the lead nucleus, with the latent heat transferred from the surroundings to providing the requisite cooling, would then, perhaps, correspond to a composition of alpha clusters (as for unstable nuclei with R>R_crit during the episode of accelerated decay) resuming the normal composition of paired nucleons but with alpha-cluster oscillations (as for stable nuclei with R≤R_crit being essentially unaffected by accelerated decay).

One final remark regarding heat, that is, regarding the necessity o terior (core and/or mantle) resulting from accelerated nuclear decay might have triggered Catastrophic Plate Tectonics (Austin et al., 1994; Silvestru, 2012). This argument might seem incompatible with the radiohalo itself which demands for its very existence-including self-consistency with the temperature vs. depth fission track annealing data (Laney and Laughlin, 1981)-a commensurate and concurrent thermal energy absorption. However, accelerated decay also affected smaller nuclei, meaning smaller than those involved in the uranium and thorium chains. Some radioactive isotopes might not experience this phase transition, or at least not experience it to the same extent, because of their smaller size or lower neutron-to-proton ratio, etc. As a result, some accelerated decay, perhaps from isotopes in the middle of Figure 2, might produce excess heat (sufficient to pull this trigger?) even if the ones for heavier isotopes do not. In any case, an episode of accelerated decay being coincident with the Flood geologically, God's purpose for it morally surely connects to executing His decreed judgment (Gen. 6:5-8) and, perhaps, by triggering its onset.

Summary

To reiterate, a phase change for the condensed matter comprising large nuclei is proposed as a heat sink during accelerated nuclear decay, being particularly relevant to the formation of radiohalos. The proposed nuclear phase change would occur in ²⁰⁶Pb nuclei, being the final stable progeny in the ²³⁸U decay chain. With each cascade of decays, the latent heat for this presumed first-order phase transition would be taken from (via heat transfer, generically invoked) and thereby continuously cool the radio-center's immediate environment wherein the thermal energy is deposited. This was explained in Part 1. Arguing by analogy with atomic/molecular systems, the plausibility of providing sufficient cooling (absorbing enough energy) by a phase change was here further explored: latent heat of an MeV per alpha cluster for arguably 41 α clusters in lead's nucleus is roughly commensurate with the 43.7 MeV of heat produced in stopping the eight alpha particles emitted in the uranium decay series. The lower-entropy phase for large, unstable nuclei during accelerated decay might consist of alpha clusters as compared with primarily nucleon pairings for the normal phase. The phase change would occur with/at the switch from unstable parent isotope to stable daughter in accordance with the dependence of a hypothetical nuclear-phase diagram on the decreased strength of the nuclear force (shallower nuclear potential) for unstable nuclei characterizing an episode of accelerated decay as compared with normalcy. Importantly, the unstable nuclides are assumed to move to the lower-entropy state, and back again, without any thermodynamic effects for the miraculous change in the strong force that turns accelerated decay on, and off, or else there is no solution.

The author hopes to explore the phase behavior of lead's nucleus by Molecular Dynamics and/or Monte Carlo simulation using a Stillinger-Weber-like potential and a small/finite ensemble of nucleons pairs (N~82 or 41 pairs of pairs) where the parameter λ (not the decay constant) for the many-body term in the potential characterizing the nuclear strength is related if not equal to the ratio R  of the binding energy per nucleon of the alpha particle to the binding energy per nucleon of the isotope, giving the higher-entropy (liquid) phase if R<R_crit and the lower-entropy (unknown) phase if R>R_crit where R_crit is near unity. Obviously, the trick is just how to model the nuclear force acting between/among nucleon pairs n↑n↓ and p↑p↓ as  oppositely "charged" molecules (speaking by analogy with molten salts) including the pairwise potential V₂ and the many-body contribution λV₃ . To this end, the author invites help in devising an appropriate model potential.

 

References

Adams, F.C., and E. Grohs. 2016. Stellar helium burning in other universes: A solution to the triple alpha fine-tuning problem. (Cornell University) arxiv: 1608.04690.

Akahane, K., J. Russo, and H. Tanaka. 2016. A possible four-phase coexistence in a single-component system. Nature Communications 7:12599; https://doi.org/10.1038/ncomms12599.

Austin, S.A, J. Baumgardner, D.R. Humphreys, A.A. Snelling, L. Vardiman, and K. Wise. 1994. Catastrophic Plate Tectonics: A global Flood model of Earth history. In Walsh, R.E. (editor). Proceedings of the Third International Conference on Creationism, pp. 609-621. Creation Science Fellowship, Pittsburgh, PA.

Breaux, G., R. Benirschke, and M. Jarrold. 2004. Melting, freezing, sublimation, and phase coexistence in sodium chloride nanocrystals. The Journal of Chemical Physics 121(13):6502; https://doi.org/10.1063/1.1786921 .

Chaffin, E.F. 2005. Accelerated Decay: Theoretical Considerations. In Vardiman, L., A. Snelling, and E.F. Chaffin (editors). Radioisotopes and the Age of the Earth, Volume II, pp. 527-533. Institute for Creation Research, El Cajon, CA, and Creation Research Society, Chino Valley, AZ.

Duarte, D., and P.B. Siegel. 2010. A potential model for alpha decay. American Journal of Physics 78(9):949; https://doi.org/10.1119/1.3432752 .

Jabes, B.S., D. Nayar, D. Dhabal, V. Molinero, and C. Chakravarty. 2012. Water and other tetrahedral liquids: Order, anomalies and solvation. Journal of Physics: Condensed Matter 24(28):284116; DOI: 10.1088/0953-8984/24/28/284116 .

Laney, R., and A.W. Laughlin. 1981. Natural annealing of the pleochroic haloes in biotite samples from deep drill holes, Fenton Hill, New Mexico. Geophysical Research Letters 8(5):501-504.

Meyerhof, W.E. 1967. Elements of Nuclear Physics. McGraw-Hill, New York, NY.

Silvestru, E. 2012. Thermal isostasy-A new look at its potential to advance diluvial geology. Journal of Creation 26(1):13-14.

Tonozuka, I., and A. Arima. 1979. Surface α-clustering and α-decays of 212Po. Nuclear Physics A 323(1):45-60.

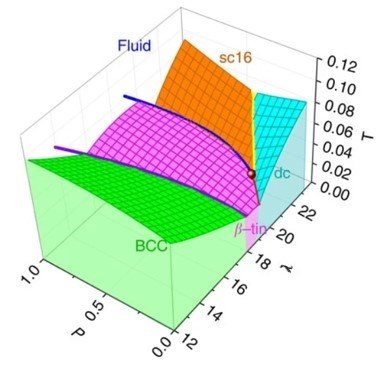
Figure 1. "The λ-P-T phase diagram. The green, pink, turquoise and orange surfaces are liquid-BCC, liquid-β-tin, liquid-dc and liquid-sc16 coexistence surfaces…" (Akahane, 2016, Fig. 1(a), used in accordance with federal copyright fair use doctrine without implying endorsement of copyright holder).

This figure is included as a generic example from the literature of modeling phase behavior for an atomic/molecular system using a Stillinger-Weber model potential that parametrizes the interaction. Here the low-entropy phases are BCC, β-tin, dc, and sc16 solids (marked by their different crystal structures), and the high-entropy phase is a liquid (i.e., a condensed fluid).

 

 

 

 

 

 

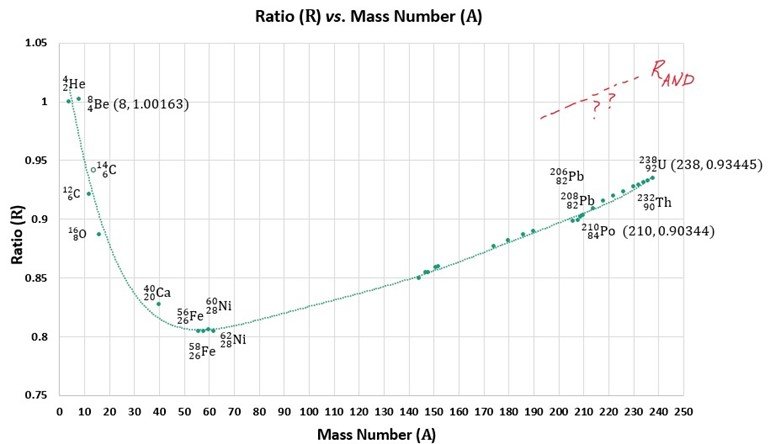
Figure 2. In this graph of the ratio 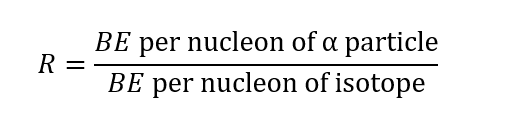vs. mass number A, note that R lies below ²³⁸U's value of 0.93445 for all the 4n nuclides (except for the highly unstable ⁸Be and the alpha particle ⁴He for which R is unity by definition), and for all the stable isotopes weightier than ¹²C as well as all primordial isotopes and decay chain products that undergo alpha decay including ²³²Th and the various poloniums.

An increase in R during an episode of accelerated decay as hypothesized would push this curve upward, and a just-so increase would put its tail (after the stable isotopes of lead) above the phase-critical value at/near unity, as for the dashed red line. This cannot be a uniform translation of the curve across all A though the change in R should be similar locally.

 

 

 

 

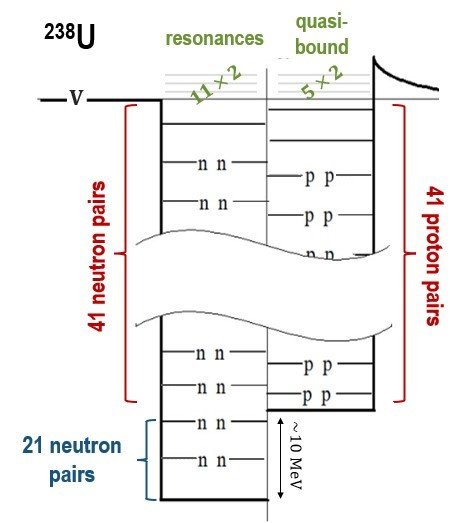
Figure 3. Schematic depiction of uranium-238 during accelerated nuclear decay, hypothesizing as unbound all decay products in the uranium series. From the nuclear surface inward (geometrically and energetically), think quasi-bound protons and resonant neutrons with small positive energies, then bound nucleons with increasingly negative energies, filling separate neutron and proton wells per the nuclear shell model for a nucleus in its ground state, as shown schematically for with stable core.

 

 

 

 

 

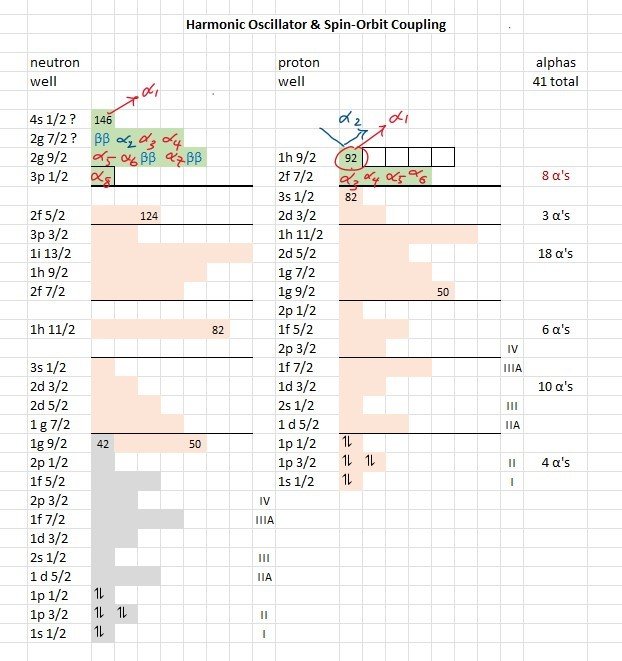
Figure 4. Placing the 146 neutrons and 92 protons for by pairs in their respective Nuclear Shell Model levels per the usual filling rules for the Harmonic Oscillator with Spin-Orbit Coupling suggests which nucleon pairs, having similar energies, might organize into as many as 41 bound alpha particles (the red boxes) for , lying below the 22 neutrons and 10 protons destined to escape (the green boxes) but above the 21 neutron pairs (the blue boxes) on bottom.

 

 

 

Footnotes:

---